Характер по группе: Гороскоп: как по группе крови определить характер человека

Гороскоп: как по группе крови определить характер человека

Согласно корейскому гороскопу, все люди делятся на четыре типа в соответствии с их группой крови. По мнению астрологов, каждая из них является не только физиологическим показателем, но и влияет на характер носителя, формирует определенный тип личности.

Тип O (I группа) — охотники

Корейский гороскоп именует людей с этой группой крови охотниками. Они энергичны, общительны, целеустремленны, обладают внутренней силой. Представители этой группы привыкают со временем полагаться только на себя, их также отличает трезвость мышления, которая не теряется даже в экстренных ситуациях.

Невероятная трудоспособность, смелость и неизменный оптимизм помогают обладателям I группы крови всегда добиваться своего, зачастую они становятся успешными в материальном плане в довольно молодом возрасте. Планы счастливчиков может нарушить свойственная им непоследовательность, а отношения с близкими часто страдают от излишней прямолинейности. Идеальным партнером для них будет человек со II или III группой крови.

Тип A (II группа) — хозяева

Хозяева воистину терпеливы, а их спокойствие нерушимо. Они тоже усердны и трудолюбивы, поэтому не бросают своих дел на полпути, и все доводят до конца. Особо нежные чувства в этих людях пробуждает понятие «дом». Они готовы бесконечно облагораживать свое жилище, стараются наладить гармоничные отношения с членами семьи, чтобы их владения были как в поговорке — крепостью с теплым очагом внутри.

Они также очень справедливы и объективны по отношению к окружающим, хотя порой с трудом приступают к новому проекту или долго не решаются действовать. Важной задачей для них является следующее — нужно научиться качественно отдыхать и расслабляться. Лучше всего в компании человека I группой крови.

Тип B (III группа) — странники

Странники — товарищи крайне сдержанные и закрытые. Они не будут демонстрировать свои истинные чувства даже в моменты, когда эмоции их переполняют. Да, несмотря на внешнюю холодность, они очень творческие, впечатлительные и переменчивые натуры. Общество сильно воздействует на их самоощущение и настроение, они легко поддаются влиянию.

Несмотря на ветреность, обладатели III группы умеют принимать решения самостоятельно и следовать им до конца, даже при осуждении со стороны. Их трудно удержать на месте, привязать к себе, выдернуть из внутреннего мира грез и фантазий — отсюда и прозвище. Идеальная пара — человек с IV группой крови.

Тип AB (IV группа) — философы

Люди с IV группой очень романтичны, но при этом обладают сильными лидерскими способностями. Настоящие интуиты и дипломаты, они всегда находят общий язык с окружающими, что помогает и в личной жизни, и в карьере. Очаровательные философы интеллигентны, незлопамятны и остроумны, но с трудом делают выбор и принимают решения.

Кроме того, очень часто обладатели IV группы теряют связь с реальностью — отказываются принимать факты, когда переполнены эмоциями. Оттого поступки могут быть необдуманными и чреватыми неприятными последствиями.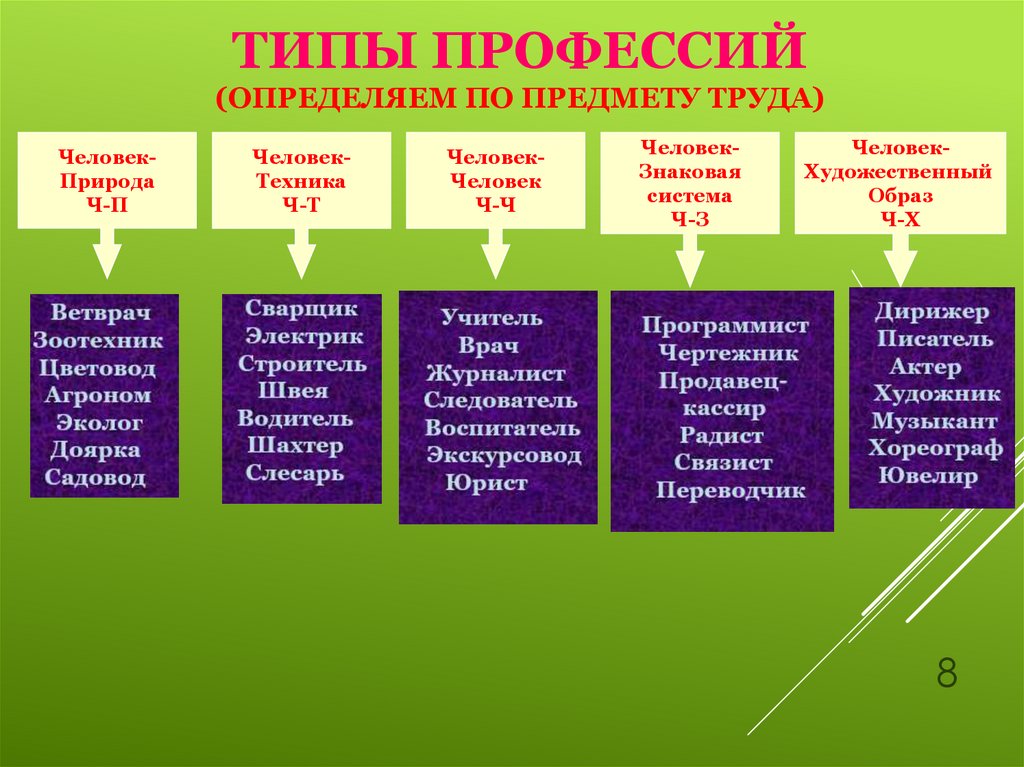 Идеальной парой для философа станет только такой же философ.

Ранее 5-tv.ru сообщал, что астрологи назвали идеальную совместимость имен для крепкого брака.

Японская теория судьбы: как группа крови влияет на характер человека | Статьи | 09.09.2022

09 сентября 2022, 07:00

Затворник, начальник и идеальный исполнитель. Кто ты по группе крови?

Читать ren.tv в

Японские ученые утверждают, что группа крови отражается на характере человека, поэтому кандидатов с третьей группой, которых считают необязательными, стараются не брать на работу. Жители Страны восходящего солнца с помощью анализов подбирают себе профессию и вторую половинку. Как узнать, кто ты, по группе крови? О тайнах крови расскажет программа «Невероятно интересные истории» на РЕН ТВ.

Одиночество в крови

Японские ученые обнаружили в плазме затворников компоненты, вызывающие склонность к депрессии и социофобии. Исследователи уверены: если снизить концентрацию этих веществ препаратами – можно вылечить так называемых хикикомори.

«Явление хикикомори, которое сейчас вызывает тревогу специалистов, социологов в Японии, заключается в том, что люди добровольно уходят в самоизоляцию. То есть они могут месяцами, годами не выходить – не то что из своей квартиры, а даже из своей комнаты. И почему это явление вызывает тревогу? Потому что на 127 миллионов жителей Японии уже достоверно зарегистрировано около миллиона таких вот затворников», – отметила психолог Евгения Евдокимова.

Японцы верят: по группе крови можно узнать многое о человеке. Поэтому о ней спрашивают при устройстве на работу и даже на первом свидании. Такой вопрос в стране Восходящего солнца никого не смущает.

«Считается, что группа крови может способствовать удаче в семейной жизни, может правильный выбор, например, партнера с правильной группой крови, может сохранить и укрепить семью. Может способствовать правильному выбору профессии», — отметил историк Станислав Рузанов.

Теория Тошитака Номи

Впервые эту теорию выдвинула японский врач Тошитака Номи. 50 лет назад она сопоставила характеры пациентов с группами крови и предположила, что обладатели первой – более энергичные, второй – предусмотрительные, третьей – творческие, а четвертой – общительные.

Но в Стране восходящего Солнца теорию Тошитаки Номи перевернули с ног на голову. Японцы стали определять свой образ жизни и принимать судьбоносные решения, исходя из группы крови. Местные производители зарабатывают на этом миллионы.

«Люди с разными группами крови покупают различные товары – бытовую технику, шоколад и прочее – для того, чтобы поддерживать свой образ жизни, связанный с их определенной группой крови», — сказал Станислав Рузанов.

Крупные компании отказались нанимать обладателей третьей группы крови. Якобы они слишком хаотичные и необязательные. А должность руководителя получают только соискатели с первой группой. Их считают прирожденными лидерами.

Что означает каждая группа крови?

Японцы верят, что черты характера личности неразрывно связаны с группой крови. Так обладатели I группы считаются общительными, предприимчивыми и смелыми. По мнению жителей Страны восходящего солнца, они ставят для себя высокие стандарты и делают все возможное, чтобы их достичь. Помимо этого, обладатели первой группы имеют лидерские качества, щедры и добросердечны. Они гибкие и могут хорошо адаптироваться даже к сложным ситуациям.

По японской теории, индивиды со второй группой крови умные, страстные, чувствительные и готовы к сотрудничеству. Это верные и терпеливые люди, любящие мир. Порой они могут быть чрезмерно чувствительны к разным вещам. Например, обладатели второй группы крови заботятся о социальных стандартах, которые не желают нарушать, и этикете.

Фото: © Скриншот видео

Согласно мнению японцев, личности с третьей группой крови очень творческие. Они очень быстро принимают решения и не умеют подчиняться приказам. Эти люди сосредотачиваются на своей цели, даже если она кажется недостижимой, сосредотачиваются на ней и никогда от нее не отказываются, как бы ни было трудно. У людей с III группой крови часто присутствует стремление быть лучшими в своем деле.

По теории японцев, характер людей с четвертой группой крови сложный и неоднозначный. Например, они могут быть одновременно общительными и застенчивыми. Считается, что обладатели самой редкой группы крови скрывают свою истинную личность от посторонних. При этом они обаятельные и легко заводят друзей, а в компании с ними никогда не скучно.

Новые группы крови

Ученые американского университета Вермонта доказали в своем исследовании, что групп крови на самом деле не четыре, а шесть. Две новые группы выявили при помощи масс-спектрометрии. Этот метод показал на поверхности эритроцитов протеины ABCB6 и ABCG2. Оба транспортных белка принимают активное участие в переносе и выводе веществ из живой клетки. Именно по ним и определяются группы крови. 

Более доскональное исследование крови началось, когда в середине прошлого века жительница Нью-Йорка внезапно скончалась после переливания. Причину смерти выясняли 60 лет, и только недавно ученым удалось разгадать эту тайну.

«Совсем недавно сделали, как они сами это заявляют, революционное открытие, связанное с тем, что они выявили якобы еще две имеющиеся группы крови», — отметил Станислав Рузанов.

Фото: © Скиншот видео

Новые группы крови назвали «Лангерайс» и «Джуниор». По словам руководителя исследования Брайана Баллифа, они встречаются крайне редко, и в основном у представителей определенных народов.

«Более 50 тысяч японцев имеют Джуниор с отрицательным резус-фактором, поэтому могут столкнуться с проблемами при переливании крови и с несовместимостью матери и плода», — сказал профессор биологии университета Вермонта Брайан Баллиф.

По мнению исследователя, науке неизвестны еще 10-15 групп крови. И пока их не открыли, людям лучше консервировать собственный биоматериал в криокамере и при необходимости использовать его вместо донорского.

Самые загадочные и интересные места нашей планеты, поразительные обычаи народов, невероятные истории и многое другое – в программе НИИ на РЕН ТВ.

групповой символ в nLab

Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |

Контекст

Теория представлений

Теория представлений

Геометрическая теория представлений

Ингредиенты

• линейная алгебра, 90 алгебра, высшая2

Определения

представление, 2-представление, ∞-представление

• группа, ∞-группа

• групповая алгебра, алгебраическая группа, алгебра Ли

• векторное пространство, n-векторное пространство

• аффинное пространство, симплектическое векторное пространство

• действие

  , действие ∞

• модуль

  , эквивариантный объект

• бимодуль, эквивалент Морита

• индуцированное представление, взаимность Фробениуса

• гильбертово пространство, банахово пространство, преобразование Фурье, функциональный анализ

• Орбита

  , коприсоединенная орбита, форма Киллинга

• унитарное представительство

• геометрическое квантование, когерентное состояние

• цоколь, колчан

• модульная алгебра, комодульная алгебра, действие Хопфа, измерение

Геометрическая теория представлений

• D-модуль, извращенная связка,

• Группа Гротендика, лямбда-кольцо, симметрическая функция, формальная группа

• главное расслоение, торсор, векторное расслоение, алгеброид Атьи Ли

• геометрическая теория функций, группоидификация

• Категория Эйленберга-Мура, алгебра над операдой, категория, скрещенный модуль

• теоремы реконструкции

Теоремы

• Теорема Бореля-Вейля-Ботта

• Be?linson-Bernstein локализация?

• Теория Каждана-Люстига

• Теорема разложения BBDG

Изменить эту боковую панель

Теория групп

Теория групп

• группа, ∞-группа
• групповой объект, групповой объект в (∞,1)-категории
• абелева группа, спектр
• суперабелева группа
• групповое действие, ∞-действие
• представление, ∞-представление
• прогруппа
• однородное пространство

Классические группы

• общая линейная группа

• унитарная группа

  • специальная унитарная группа. проективная унитарная группа

• ортогональная группа

  • специальная ортогональная группа

• симплектическая группа

Конечные группы

• конечная группа

• симметричная группа, циклическая группа, группа кос

• классификация конечных простых групп

• спорадические конечные простые группы

  • Группа монстров, группа Матье

Групповые схемы

• Алгебраическая группа
• абелева разновидность

Топологические группы

• топологическая группа

• компактная топологическая группа, локально компактная топологическая группа

• максимальная компактная подгруппа

• группа строк

Группы Ли

• Группа Ли

• компактная группа Ли

• Группа Кац-Муди

Группы супер-Ли

• супер группа Ли

• суперевклидова группа

Высшие группы

• 2 группы

  • модуль перекрестный, строгий 2-х групповый

• н-группа

• ∞-группа

  • симплициальная группа

  • скрещенный комплекс

  • k-тупый групповой n-группоид

  • спектр

• круг n-группа, струна 2-группа, пятигранник Ли 6-группа

Когомологии и расширения

• групповые когомологии

• Групповое расширение

  ,

• ∞-группа расширения, Ext-группа

• квантовая группа

Изменить эту боковую панель

• Идея
• Свойства
• Ограничение групповых символов максимальными торами – веса
• Связь с корнями Черна и принцип расщепления
• Характеры и фундаментальная группа торов 9\раз, Г).

  Для топологических групп рассматриваются непрерывные характеры. В частности, для локально компактной хаусдорфовой группы GG (часто в дальнейшем предполагается, что это абелева группа) характер группы GG является непрерывным гомоморфизмом в группу окружностей ℝ/ℤ\mathbb{R}/\mathbb{Z}. Если GG проконечна, то это то же самое, что непрерывный гомоморфизм в дискретную группу ℚ/ℤ\mathbb{Q}/\mathbb{Z}. (См. MO.)

  Свойства

  Ограничение групповых символов максимальными торами – веса 91] \,.

  Внутренний продукт и ортогональность

  Комплексные функции класса на конечной группе GG имеют скалярный продукт, заданный выражением

  ⟨α,β⟩≔1|G|∑g∈Gα(g)β(g)¯. \лангле\альфа,\бета\рангл \coloneqq \ гидроразрыва {1} {{\ vert G \ vert}} \ underset {g \ in G} {\ sum} \ alpha (g) \ overline {\ beta (g)} \,.

  Отношение ортогональности Шура — это утверждение о том, что неприводимые групповые характеры {χi}i\{\chi_i\}_i образуют ортонормированный базис пространства функций классов относительно этого скалярного произведения: 90(\mathcal{L} В G, \mathbb{C}). Эта конструкция полезна при обобщении на трансхроматические символы.

  • Двойственность Понтрягина, Двойственность Понтрягина

  • класс сопряженности подгрупп

  Ссылки

  Оригинальные статьи о кольцах характеров/кольцах представлений компактных групп Ли включают

  • Грэм Сегал, Кольцо представлений компактной группы Ли , Publications Mathématiques de l’Institut des Hautes Scientifiques, 19 января68, том 34, выпуск 1, стр. 113-128 (номер: PMIHES_1968__34__113_0)

  • Masaru Tackeuchi, Замечание о кольце характеров компактной группы Ли , J. Math. соц. Япония, том 23, номер 4 (1971), 555–705 (евклид: jmsj/1259849785)

  Конспекты лекций о характерах конечных и компактных групп Ли включают

  • Troels Roussauc Johansen, Теория характеров для конечных групп и компактных групп Ли pdf

  • Андрей Яфаев, Характеры конечных групп (pdf)

  Обсуждение конечных групп в более общем контексте эквивариантной комплексно-ориентированной теории когомологий (трансхроматический характер) находится в

  • Майкл Хопкинс, Николас Кун, Дуглас Равенел, Обобщенные групповые характеры и комплексно-ориентированные теории когомологий
    , J. Amer. Мат. соц. 13 (2000), 553-594 (издатель, pdf)

  Последняя редакция: 27 апреля 2021 г., 12:49:26. См. историю этой страницы для получения списка всех вкладов в нее.

  р — Как сгруппировать персонажей

  спросил 4 года, 6 месяцев назад

  Изменено 4 года, 6 месяцев назад

  Просмотрено 2к раз

  У меня есть фрейм данных с двумя столбцами. Один из них является именем группы, а другой содержит следующие значения для группы. Фактический список намного длиннее

   Моя группа привет
  Моя группа до свидания
  Добрый день, моя группа
  Ваша группа красный
  Ваша группа синий
  Ваша группа зеленый
   

  Я хотел бы создать следующий вывод:

   Моя группа<-c("привет","до свидания","бонжур")
  Ваша группа<-c("красный","синий","зеленый")
   

  Можно ли это сделать с помощью группы в dplyr или есть другой способ получить желаемый результат?

  1

  Можно использовать гнездо от тідыр :

   библиотека (tidyverse)
  data_out <- данные %>%
    group_by(группы) %>%
    гнездо()
   

  Вы можете получить доступ к своим группам, выполнив:

   data_out$data
  #[[1]]
  # Таблетка: 3 x 1
  # слова
  # <фкт>
  #1 привет
  #2 до свидания
  #3 Добрый день
  #[[2]]
  ## Таблетка: 3 x 1
  # слова
  # <фкт>
  #1 красный
  #2 синий
  #3 зеленый
   

  Вы можете использовать функцию split , чтобы разделить данные на основе групп , а затем использовать unique , чтобы получить список уникальных строк или значений

   разделенный <- разделенный (df, f = группы данных $)
  уникальный (разделенные $ MyGroup $ слова)
  уникальный (разделенные $ YourGroup $ слова)
  #>
    разделенный <- разделенный (df, f = data$groups)
  #> уникальный(разделенные слова$MyGroup$)
  #[1] привет, добрый день
  #Уровни: синий бонжур зеленый привет красный
  #> уникальный(разделенные слова$вашейгруппы$)
  #[1] красный синий зеленый
  #Уровни: синий бонжур зеленый привет красный
   

  Примечание: я заменил прощай на другой здравствуй чтобы результаты были понятны, ты видишь только один здравствуй присутствует.