Что такое циклоид: ЦИКЛОИДА | это… Что такое ЦИКЛОИДА? — samara-history.ru

Что такое циклоид: ЦИКЛОИДА | это… Что такое ЦИКЛОИДА?

Содержание

ЦИКЛОИДА | Энциклопедия Кругосвет

ЦИКЛОИДА (в переводе с греч. кругообразный) – плоская трансцендентная кривая, которую описывает точка окружности радиуса r, катящейся по прямой без скольжения (трансцендентной кривой называется кривая, которая в прямоугольных координатах не может быть описана алгебраическим уравнением). Ее параметрическое уравнение

x = rt – r sin t,
y = r – r cos t

Точки пересечения циклоиды с прямой, по которой катится окружность (эта окружность называется производящей, а прямая, по которой она катится, – направляющей), называются точками возврата, а самые высокие точки на циклоиде, расположенные посредине между соседними точками возврата, называются вершинами циклоиды.

Первым изучать циклоиду начал Галилео Галилей. Длина одной арки циклоиды была определена в 1658 английским архитектором и математиком Кристофером Реном, автором проекта и строителем купола собора Святого Павла в Лондоне. Оказалось, что длина циклоиды равна 8-ми радиусам производящей окружности.
Одно из замечательных свойств циклоиды, давшее ей название – брахистохрона (от греческих слов «кратчайший» и «время) связано с решением задачи о наискорейшем спуске. Встал вопрос, какую форму надо придать хорошо отшлифованному (чтобы практически исключить трение) желобу, соединяющему две точки, чтобы шарик скатился вниз от одной точки к другой в кратчайшее время. Братья Бернулли доказали, что желоб должен иметь форму опрокинутой вниз циклоиды.

Родственные циклоиде кривые можно получить, рассматривая траектории точек, не находящихся на производящей окружности.

Пусть точка С₀ находится внутри окружности. Если провести через С₀ вспомогательную окружность с тем же центром, что и у производящей окружности, то при качении производящей окружности по прямой АВ маленькая окружность будет катиться по прямой A´В´, но ее качение будет сопровождаться скольжением, и точка С₀ описывает кривую, называемую укороченной циклоидой.

Аналогичным образом определяется удлиненная циклоида – это траектория точки, расположенной на продолжении радиуса производящей окружности, при этом качение сопровождается скольжением в противоположном направлении.

Циклоидальные кривые применяются при многих технических расчетах и свойства их используются, например, при построении профилей зубьев шестерен, в циклоидальных маятниках, в оптике и, таким образом, изучение этих кривых важно с прикладной точки зрения. Не менее важно и то, что, изучая эти кривые и их свойства, ученые 17 в. разрабатывали приемы, которые привели к созданию дифференциального и интегрального исчислений, а задача о брахистохроне явилась шагом к изобретению вариационного исчисления.

Елена Малишевская

Проверь себя!
Ответь на вопросы викторины «Математика»

Как звали математика, который в 19 лет решил задачу, не поддававшуюся усилиям лучших геометров со времен Евклида?

Пройти тест

Циклоида / Этюды // Математические этюды

Математические этюды

К списку

Помните оранжевые пластмассовые катафоты — светоотражатели, прикрепляющиеся к спицам велосипедного колеса? Прикрепим катафот к самому ободу колеса и проследим за его траекторией. Полученные кривые принадлежат семейству циклоид.

Колесо при этом называется производящим кругом (или окружностью) циклоиды.

Но давайте вернёмся в наш век и пересядем на более современную технику. На пути байка попался камушек, который застрял в протекторе колеса. Провернувшись несколько кругов с колесом, куда полетит камень, когда выскочит из протектора? Против направления движения мотоцикла или по направлению?

Как известно, свободное движение тела начинается по касательной к той траектории, по которой оно двигалось. Касательная к циклоиде всегда направлена по направлению движения и проходит через верхнюю точку производящей окружности. По направлению движения полетит и наш камушек.

Помните, как Вы катались в детстве по лужам на велосипеде без заднего крыла? Мокрая полоска на вашей спине является житейским подтверждением только что полученного результата.

Век XVII — это век циклоиды. Лучшие учёные изучали её удивительные свойства.

Какая траектория приведёт тело, движущееся под действием силы тяжести, из одной точки в другую за кратчайшее время? Это была одна из первых задач той науки, которая сейчас носит название вариационное исчисление.

Минимизировать (или максимизировать) можно разные вещи — длину пути, скорость, время. В задаче о брахистохроне минимизируется именно время (что подчёркивается самим названием: греч. βράχιστος — наименьший, χρόνος — время).

Первое, что приходит на ум, — это прямолинейная траектория. Давайте также рассмотрим перевёрнутую циклоиду с точкой возврата в верхней из заданных точек. И, следуя за Галилео Галилеем, — четвертинку окружности, соединяющую наши точки.

Сделаем бобслейные трассы с рассмотренными профилями и проследим, какой из бобов приедет первым.

История бобслея берёт своё начало в Швейцарии. В 1924 году во французском городе Шамони проходят первые зимние Олимпийские игры. На них уже проводятся соревнования по бобслею для экипажей двоек и четвёрок. Единственный год, когда на Олимпийских играх экипаж боба состоял из пяти человек, был 1928. С тех пор в бобслее всегда соревнуются мужские экипажи двойки и четвёрки. В правилах бобслея много интересного. Конечно же, существует ограничения на вес боба и команды, но существуют даже ограничения на материалы, которые можно использовать в коньках боба (передняя пара их подвижна и связана с рулём, задняя закреплена жёстко). Например, радий не может использоваться при изготовлении коньков.

Дадим старт нашим четвёркам. Какой же боб первым приедет к финишу? Боб зелёного цвета, выступающий за команду Математических этюдов и катившийся по циклоидальной горке, приходит первым!

Почему же Галилео Галилей рассматривал четвертинку окружности и считал, что это наилучшая в смысле времени траектория спуска? Он вписывал в неё ломаные и заметил, что при увеличении числа звеньев время спуска уменьшается. Отсюда Галилей естественным образом перешёл к окружности, но сделал неверный вывод, что эта траектория наилучшая среди всех возможных. Как мы видели, наилучшей траекторией является циклоида.

Через две данные точки можно провести единственную циклоиду с условием, что в верхней точке находится точка возврата циклоиды. И даже когда циклоиде приходится подниматься, чтобы пройти через вторую точку, она всё равно будет кривой наискорейшего спуска!

Ещё одна красивая задача, связанная с циклоидой, — задача о таутохроне. В переводе с греческого ταύτίς означает «тот же самый», χρόνος, как мы уже знаем — «время».

Сделаем три одинаковые горки с профилем в виде циклоиды, так, чтобы концы горок совпадали и располагались в вершине циклоиды. Поставим три боба на разные высоты и дадим отмашку. Удивительнейший факт — все бобы приедут вниз одновременно!

Зимой Вы можете построить во дворе горку изо льда и проверить это свойство вживую.

Задача о таутохроне состоит в нахождении такой кривой, что, начиная с любого начального положения, время спуска в заданную точку будет одинаковым.

Христиан Гюйгенс доказал, что единственной таутохроной является циклоида.

Конечно же, Гюйгенса не интересовал спуск по ледяным горкам. В то время учёные не имели такой роскоши заниматься науками из любви к искусству. Задачи, которые изучались, исходили из жизни и запросов техники того времени. В XVII веке совершаются уже дальние морские плавания. Широту моряки умели определять уже достаточно точно, но удивительно, что долготу не умели определять совсем. И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.

Первым, кто задумал делать маятниковые часы, которые были бы точны, был Галилео Галилей. Однако в тот момент, когда он начинает их реализовывать, он уже стар, он слеп, и за оставшийся год своей жизни учёный не успевает сделать часы.

Он завещает это сыну, однако тот медлит и начинает заниматься маятником тоже лишь перед смертью и не успевает реализовать замысел. Следующей знаковой фигурой был Христиан Гюйгенс.

Он заметил, что период колебания обычного маятника, рассматривавшегося Галилеем, зависит от изначального положения, т.е. от амплитуды. Задумавшись о том, какова должна быть траектория движения груза, чтобы время качения по ней не зависело от амплитуды, он решает задачу о таутохроне. Но как заставить груз двигаться по циклоиде? Переводя теоретические исследования в практическую плоскость, Гюйгенс делает «щёчки», на которые наматывается веревка маятника, и решает ещё несколько математических задач. Он доказывает, что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой циклоиды является циклоида с теми же параметрами.

Кроме того, предложенная Гюйгенсом конструкция циклоидального маятника позволяет посчитать длину циклоиды. Если синюю ниточку, длина которой равна четырём радиусам производящего круга, максимально отклонить, то её конец будет в точке пересечения «щёчки» и циклоиды-траектории, т.е. в вершине циклоиды-«щёчки». Так как это половина длины арки циклоиды, то полная длина равна восьми радиусам производящего круга.

Христиан Гюйгенс сделал циклоидальный маятник, и часы с ним проходили испытания в морских путешествиях, но не прижились. Впрочем, так же, как и часы с обычным маятником для этих целей.

Отчего же, однако, до сих пор существуют часовые механизмы с обыкновенным маятником? Если приглядеться, то при малых отклонениях, как у красного маятника, «щёчки» циклоидального маятника почти не оказывают влияния. Соответственно, движение по циклоиде и по окружности при малых отклонениях почти совпадают.

Литература

Берман Г. Н. Циклоида. — М. : Наука, 1980.

Гиндикин С. Г. Рассказы о физиках и математиках. — М. : МЦНМО, 2006.

Другие этюды раздела «Замечательные кривые»

Цепная линия Винтовая линия

Математические этюды

Cycloid Определение и значение — Merriam-Webster

1 из 2

циклоид ˈsī-ˌklȯid

: кривая, образованная точкой на окружности при движении по прямой линии

циклоидальный

си-клти-дл

прилагательное

Иллюстрация циклоиды

циклоиды

2 из 2

: гладкая с концентрическими линиями роста

циклоидные весы

также : имеющие или состоящие из циклоидной чешуи

: характеризующиеся чередованием приподнятого и пониженного настроения

циклоидная личность

Примеры предложений

Последние примеры в Интернете

Модель, выставленная в Музее Галилея, позволяет проверить этот результат, построив две дорожки: одну в форме циклоиды , другую в форме дуги окружности для сравнения. — Дженнифер Уэллетт, 9 лет.0047 Ars Technica , 17 мая 2020 г. Решением является циклоида , которая представляет собой кривую, созданную катящимся колесом по кругу. — Дженнифер Уэллетт, Ars Technica , 17 мая 2020 г.

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «циклоид». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

Существительное

Французский cycloïde , от греческого kykloeidēs круговой, от kyklos

Первое известное употребление

Существительное

1661 в значении, определенном выше Первое известное использование циклоиды было в 1661 г.

Посмотреть другие слова того же года

Словарные статьи Около

циклоида

циклогексиламин

циклоида

циклоидальный маятник

Посмотреть другие записи поблизости

Процитировать эту запись «Циклоид».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/cycloid. По состоянию на 14 января 2023 г.

Копировать цитирование

Детское определение

циклоида

существительное

циклоид

ˈsī-ˌklȯid

: кривая, описываемая точкой на окружности, катящейся по прямой линии

Медицинское определение

циклоида

1 из 2 существительное

циклоид ˈsī-ˌklȯid

: циклоидный человек

циклоидный

2 из 2 прилагательное

: относящееся к личности, характеризующейся чередованием приподнятого и плохого настроения

сравнить циклотимический

0003

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

малопонятный

См. Определения и примеры »

Получайте ежедневно по электронной почте Слово дня!

Модные слова

Какой из этих предметов назван в честь смертоносного оружия?

хенли рубашка шляпа Федора
Броги Каблук-шпилька

Прослушайте слово и напечатайте его. Сколько вы можете получить правильно?

ПРОЙДИТЕ ТЕСТ

Сможете ли вы составить 12 слов из 7 букв?

PLAY

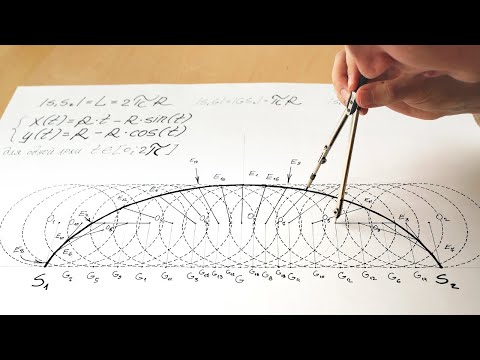
Циклоида и ее свойства Связанные кривые

Циклоида — это кривая, описываемая точкой на окружности при движении по прямой. Циклоида, образованная окружностью радиусом r , катящейся по оси x , представлена параметрическим уравнением:

$\left\{\begin{matrix} x(t)= rt — r\sin(t )\\ y(t)= r-r\cos(t)\\ \end{matrix}\right. {b}y\text{ }dx$. 9{2\pi} = -4r(-1-1) = 8r$

Длина дуги одной арки циклоиды равна 8 r или в 8 раз больше радиуса окружности, которая ее создала.

Интересно, что формула площади имеет множитель π , как площадь круга, но формула длины дуги не имеет множителя π , как длина окружности.

Объем

Объем V твердого тела, образованного вращением дуги циклоиды вокруг x 93$.

Чашка циклоиды

Каков объем циклоиды, вращающейся вокруг своей оси симметрии и имеющей форму чаши? Я придумал следующий объем, используя дисковый метод. Осью симметрии является линия х = π.

Возьмите горизонтальное поперечное сечение от 0 до π для площади круга, который будет образован вращением. Вычтите значение x из π, чтобы получить радиус этого цикла. Радиус r будет равен $R\pi — R(t-\sin(t))$, где 92}{2}-\frac{8}{3}\right)$ ≈ 38,13 R ³ . Я не смог проверить эту формулу, так как не видел циклоидного вращения в чаше. 2\cdot R\sin(t)dt$. Это соответствует тому же объему, что и выше. Этот объем казался бы разумным, если бы он был меньше объема цилиндра, созданного радиусом 93$. Объем циклоидной чашки больше половины объема цилиндра, и это кажется разумным.

Прямоугольный треугольник

Прямой угол спрятан в циклоиде. Угол возникает на пересечении циклоиды и окружности. Диаметр окружности — это гипотенуза.

На изображении выше APC представляет собой прямоугольный треугольник. Чтобы доказать это, мы можем доказать, что ортогональная касательная к циклоиде проходит через окружность, где она касается x — ось. Во-первых, давайте найдем наклон касательной к циклоиде в точке t .

(i) $ \ frac {dy} {dx} = \ frac {\ frac {dy} {dt} (r-r \ cos t)} {\ frac {dx} {dt} (rt-r \ sin t) } = $ $\frac{r\sin t}{r — r\cos t} =$ $\frac{r\sin t}{1 — \cos t}$

Наклон ортогоналя будет отрицательным обратным : $-\frac{dx}{dy} = -\frac{1-\cos t}{\sin t}$. В точке t точка на циклоиде равна $(rt — r\sin t, r — r\cos t)$. Следовательно, уравнение ортогонала:

(ii) $y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}[x — (rt — r\sin t)]$

Точка, в которой Окружность, касающаяся оси x , равна rt , потому что t на самом деле является углом, под которым окружность движется вдоль оси x . Следовательно, мы можем найти значение y , когда x равно rt , подставив x = rt в уравнение ортогонала. (Нет необходимости упрощать уравнение прямой в (ii).)

(iii) $y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}[rt — (rt — r\sin t)]$

(iv) $ y — (r — r\cos t) = \frac{\cos t — 1}{\sin t}(r\sin t)$

(v) $y — (r — r\cos t) = r \cos t — r$

(vi) $y = 0$

Следовательно, для любого t ортогональная ось всегда будет пересекать окружность в точке касания с осью x . А поскольку ортогональный угол по определению является прямым, отрезок PA должен пересечь окружность в точке A, что делает AC диаметром окружности. Если мы позволим y = 0 и решить для x , мы получим x = rt .

Циклоида и синусоида

Синусоида имеет особое отношение к циклоиде. Если мы построим график переведенной синусоиды $y = r\sin(x — \frac{\pi}{2}) + r$. Это точная синусоида, только масштабированная как r . Форма такая же, как если бы мы начертили y = sin x . Циклоида и синусоида показаны ниже.

Если мы возьмем точку P на циклоиде и проведем параллель в P, то она пересечет синусоиду в D и E и снова циклоиду в G. Отрезки PD и EG конгруэнтны в силу симметрии и равны r грех т .

Мы можем показать, что DO перпендикулярен оси x . Следовательно, сумма отрезков PD и EG равна длине хорды окружности PK для всех t . Или PK в два раза длиннее PD. Это означает, что площадь, ограниченная циклоидой и синусоидой, равна площади круга. А площадь под синусоиды равна удвоенной площади круга, так как площадь под циклоидой в 3 раза больше окружности.